Effective Elasticity tensor

Calculation of an effective elasticity tensor

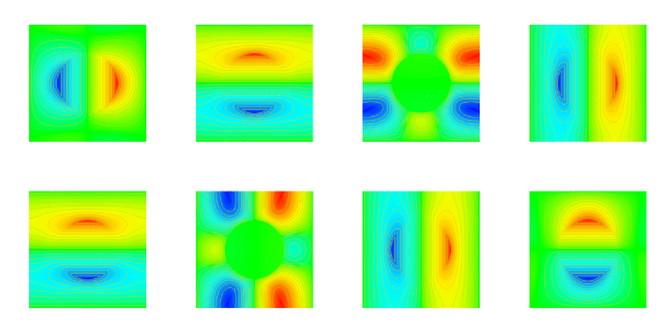
Assume that we have a two-dimensional elastic medium with periodically distributed circular inlays consisting of a stiffer material. If these holes are small then the medium will behave on a macroscopic scale like a homogeneous medium without holes. The elasticity tensor of this medium can be calculated as follows:

On the representative cell compute a tensor N of rank 3 which correspond to responses of the representative cell to different loads. Boundary conditions for this problem are periodic.
Compute the effective tensor by evaluating the load functionals on the tensor N.

The picture above shows the 8 components of the tensor N for the 2D-case.

We used conforming finite elements of order 5 with nonlinear element mappings to approximate the tensor N. Solver for the linear problems was a W(1,1)-multigrid cycle with an overlapping block Gauss-Seidel smoother.

The history of this calculation was as follows (three of the 16 components are shown, due to symmetry properties the remaining ones can be obtained by a suitable permutation of indices):

Cells	Unknowns	Matrix entries	A₁₁₁₁	A₁₂₁₂	A₁₂₂₁
9	1800	43060	4.1458940638	1.3176717343	1.2966840277
36	7200	176224	4.1412496929	1.3139564023	1.2979726371
144	28800	705600	4.1412384319	1.3139473004	1.2979716831
576	115200	2822400	4.1412383854	1.3139472825	1.2979716903
2304	460800	11289600	4.1412383853	1.3139472825	1.2979716903

Nicolas Neuss, 2017-01-31